Quantum Materials
The exotic faces of entangled electrons in solids
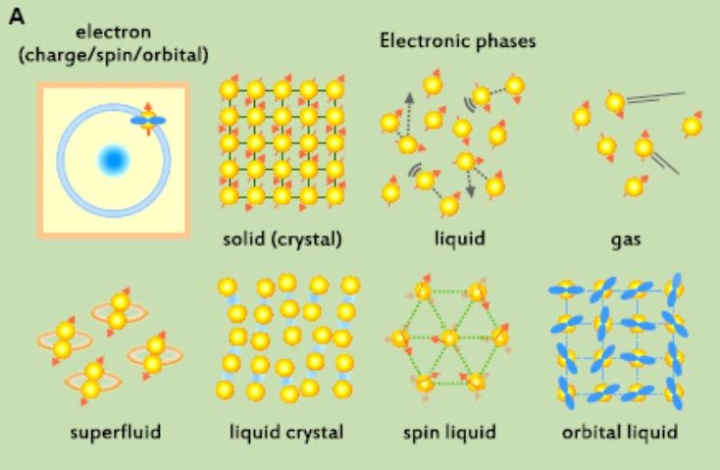
“Correlated electron systems” have long been a major topic in materials physics and chemistry. However, the field never became old since new discoveries kept coming out and captured the heart of condensed matter scientists. Entanglements of electrons due to many body interactions, in particular Coulomb repulsion, give rise to solid, liquid and gaseous states of electrons analogous to those found in interacting atoms and molecules. (Fig. 1) With the presence of the multiple degrees of freedom associated with electrons - charge, spin and orbitals - and the possible interplay between them, correlated electron systems enable a surprisingly rich variety of self-organized states of electrons (electronic phases) to emerge. Transition metal compounds, in which the d-electrons determine the electronic properties, are an attractive playground in which such exotic phase formation may be realized [1].
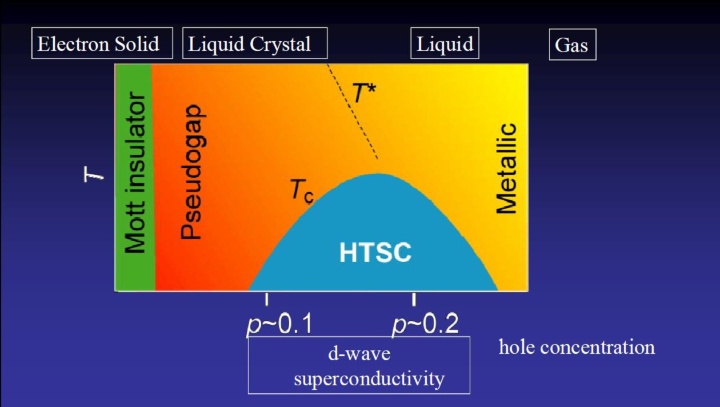
The potency of the concept of electronic phases driven by the interplay between competing electronic degrees of freedom may be illustrated by considering the phase diagram of high-Tc cuprate superconductors (see Fig. 2). The parent compound of the high-Tc cuprates is a Mott insulator with one electron in its dx2-y2 orbital, which can be viewed as an electron solid. Upon carrier doping the electron solid melts and, in the strongly entangled phase where an interplay of charge and spin degrees of freedom is anticipated, high temperature superconductivity shows up due to the formation of a superfluid of electrons. Upon further doping, the electron system becomes less entangled and superconductivity fades out and a normal gaseous phase is recovered. On the way from the electron solid to the superconducting phase, a mysterious, pseudo-gap, phase is found, which was recently discovered to be a complex self-organized “hidden” state of ordered spin and charge. Another appealing example of an exotic electronic phase is a liquid state of spins. When antiferromagnetically coupled spins are placed on a triangular lattice, it is not possible to save energy by satisfying the condition that all neighboring spins align antiparallel with each other, as demanded by the antiferromagnetic coupling between them. In combination with the quantum mechanical character of spins, this effect known as geometrical frustration, forms a nontrivial highly entropic liquid ground state of spins called a quantum spin liquid. Exotic properties including the presence of a spin Fermi surface were predicted, furthermore, quantum spin liquids themselves have been touted as the precursors for novel electronic phases. Recently, realistic candidate materials were discovered and quantum spin liquids are no longer just a toy of theorists, but a test bed in which novel theoretical concepts can be tested and explored [2].
Intriguingly, these rich electronic phases are in a delicate balance, competing with each other to play the dominant role in determining the material properties. Even a minute external impetus can tip the balance in favor of one phase over another, and therefore dramatic phase changes can result from small external perturbations. The coexistence of charge and spin degrees of freedom can bring about a cross-coupling between the electric and magnetic response. This unique feature gives rise to the possibility of phase change functions in transition metal oxides, useful as sensors, digital memory and for signal conversion. Well known examples of this approach are the so-called “colossal magnetoresistance” (CMR) devices, based on complex Mn oxides, employed as magnetic field sensors. The electronic phase change provides in addition a variety of novel functions, including entropic and mechanical functions. As a consequence of the multiple degrees of freedom, some electronic phases are highly entropic, and in fact, the change of volume enthalpy associated with an electronic phase transition is sometimes comparable to that of the water-ice transition. Applications of such large enthalpy include electronic ice packs, thermoelectric devices, and magnetic/electric refrigeration.
Recognizing the above mentioned potential of transition metal compounds, we are aiming to discover new compounds with transition metal elements in which novel, exotic and/or functional electronic phases are realized on the basis of intimate collaboration between physics and chemistry. In the recent years, one of our major playgrounds was complex oxides with heavy 5d transition elements in particular Iridium (Ir), where strong spin orbit coupling in addition to the electron correlations can enrich the electronic phases with novel topological effects.
Spin-orbit coupling links spin of electrons with motion of electrons, where one of the spin state (up or down) is preferred by the electrons moving towards the specific direction, and plays crucial role in spintronics. Since it is a relativistic effect, the heavier the atom is, the stronger the coupling is. In heavy 5d transition metal ions such as iridium, the energy scale of spin-orbit coupling is as large as 1 eV, comparable with those of the band width W (~kinetic energy) and the Coulomb repulsion between electrons U. The competition and/or interplay of spin-orbit coupling with the other two may alter the landscape of electronic structure completely. Along this line, we have first identified spin-orbital Mott insulator, a novel electron solid in a layered perovskite Sr2IrO4 [3,4], and then developed further exotic electronic phases, including a Dirac node semimetal, in perovskite SrIrO3 [5] and possible Kitaev spin liquid state in honeycomb base Li2IrO3 [6].
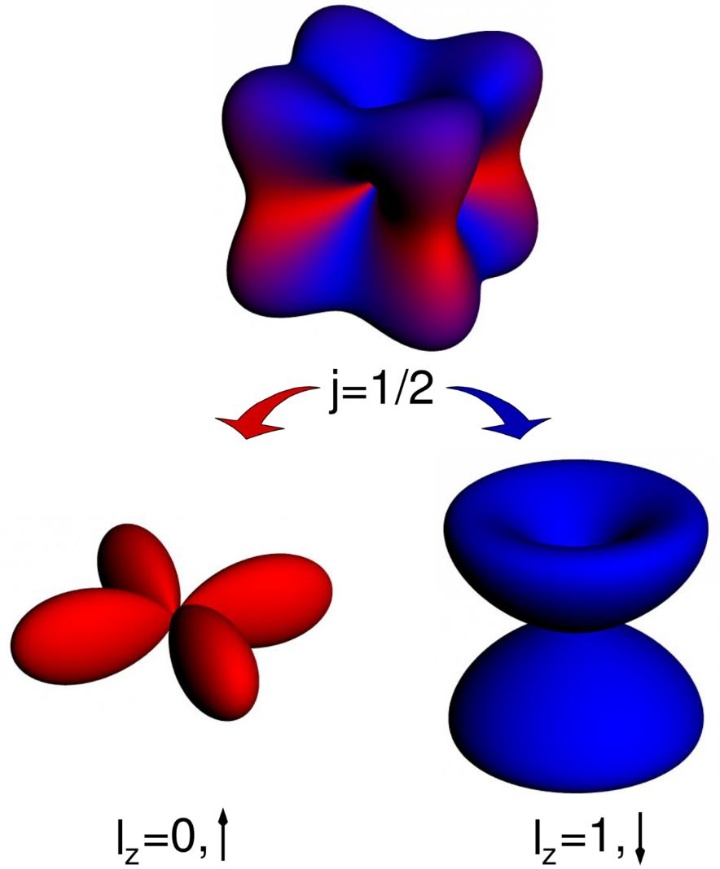
5d transition metal compounds are generally believed to be more itinerant than their 3d and 4d analogues. A layered oxide Sr2IrO4 with Ir4+(5d5), however, is known to be an antiferromagnetic Mott insulator despite its 4d analogue Sr2RhO4 is simply a paramagnetic metal. It was pointed out that the Mott insulating state in this Sr2IrO4 is induced by a very strong SOC of ~ 0.7 eV. The large SOC forces electrons in 5d orbital to recover orbital motion by mixing up three anisotropic orbital states xy, yz and zx. This state is called Jeff = 1/2 state. The formation of a half filled and narrow Jeff=1/2 band leads to a Mott insulting state (electron solid) even in the presence of a weak U~0.5 eV [3]. From a “selection rule” of the magnetic resonant x-ray scattering at Ir L-edge, we unambiguously demonstrated [4] that the ground state of Sr2IrO4 is a antiferromagnet made of Jeff=1/2 isospins, evidencing the spin-orbital Mott state. The magnetism of Jeff=1/2 moment in Sr2IrO4 is somewhat unexpected. In the textbook of magnetism, spin-orbit coupling is described as a source of magnetic anisotropy. Despite the strong spin-orbit coupling, the magnetism of Jeff=1/2 iso-spins in Sr2IrO4 was found to be surprisingly isotropic rather than anisotropic. It is due to the admixture of different orbital states in Jeff=1/2 moment, which may be viewed as spin-orbit coupling induced isotropy [7]. The temperature dependence of in-plane magnetic correlation length of Jeff=1/2 iso-spins, obtained from inelastic x-ray resonant magnetic scattering, was indeed well described by that expected for two-dimensional and isotropic S=1/2 Heisenberg antiferromagnet [8], just like the mother compound of high-Tc superconducting copper oxides.
The three-dimensional analog of Sr2IrO4, SrIrO3, distorted perovskite, is not a spin-orbital Mott insulator but a correlated Dirac node semimetal, an electron gas with zero mass [9], likely due to the reduced correlation effects associated with the three dimensionality. All the results of transport measurements were consistent with the presence of Dirac electrons in the three-dimensional iridium oxide. The presence of Dirac electrons are like graphene but, in iridium oxide, Dirac electrons are strongly correlated. Using (SrIrO3)m/SrTiO3 (m: number of SrIrO3 layers) super-lattice structure on SrTiO3 (001) substrate, we could have controlled successfully the dimensionality and hence increasing effective Coulomb U [5]. With decreasing the number of SrIrO3 layers, we observe a Dirac semimetal to insulator transition at m=3, accompanied with the onset of canted antiferromagnetism. This can be understood as a gapping of the Dirac nodes by breaking time reversal symmetry with magnetic moments. At m=1, the single layer, the transport remains insulating even above the magnetic ordering temperature, indicative of the increased spin-orbital Mott character as in Sr2IrO4.
Realization of quantum spin liquids is a long sought-after dream in condensed matter physics. Geometrically frustrated antiferromagnets with a triangular-based lattice have been discussed to be the most promising arena for spin liquids. A few organic and inorganic compounds with triangular based structure have been pointed out to be the materialization of quantum spin liquid but the ground state of those compounds are still subject of debates. Kitaev spin liquids on honeycomb lattice are based on bond-dependent ferromagnetic interactions, distinct from geometrically frustrated antiferromagnet, in that the presence of spin liquid state was theoretically and rigorously proven, and may bring a new paradigm in the science of quantum spin liquid [10]. α-A2IrO3 (A = Li, Na) was discussed to be a possible realization of a “Kitaev spin liquid” [7]. It has a network of edge-sharing IrO6 octahedra, which could give rise to a Kitaev-type magnetic coupling associated with the interference effect unique to the spin-orbital entangled Jeff = 1/2 state. The results of physical property measurements on the honeycomb iridates, however, indicated an antiferromagnetic transition rather than spin liquid state, likely due to the presence of additional antiferromagnetic interactions and lattice distortion. In order to realize a Kitaev spin liquid, materials with dominant Kitaev-type ferromagnetic interactions are highly desired.
We discovered a new iridium oxide β-Li2IrO3 which comprises edge-sharing network of IrO6 octahedra in the three dimensions [6]. Each Ir4+ ion has three 120°-bonds to the neighboring Ir4+ ions as in honeycomb structure. (Fig. 4) We named the three-dimensional analogue of the honeycomb lattice as “hyperhoneycomb” lattice. The hyperhoneycomb lattice was theoretically shown to be the platform for Kitaev spin liquid as well as 2D honeycomb lattice.
The magnetic measurements of β-Li2IrO3 at ambient pressure indicated dominant Kitaev-type ferromagnetic interactions in contrast to α-Li2IrO3. A magnetic ordering, however, was again observed at 38 K and a complicated non-collinear arrangement of Jeff=1/2 spins is realized rather than the desired quantum spin liquid state. The signature of proximity to a ferromagnetism and the presence of large fluctuations suggest that the observed ordered state of β-Li2IrO3 is very close to Kitaev spin liquid. In fact, by applying pressure of 2GPa, we recently found that the signature of ordering goes away and spin liquid-like phase is realized [6]. This suggests that newly discovered β-Li2IrO3 may reach the holy grail, a quantum spin liquid.
Exploration of novel phases of correlated electrons has long been a major topic of condensed matter physics. Despite three decades of research, always new phases and concepts have been born out of correlated electrons. By adding strong relativistic spin orbit coupling to electron correlations using complex iridium oxides as a playground, as we discussed in the short review, novel phases of correlated electrons were discovered, including spin orbital Mott insulator, correlated Dirac node semimetal, and Kitaev quantum spin liquid. Clearly, it is a rich mine to be explored further.
- Takagi, H.; Hwang, H. Y.
An Emergent Change of Phase for Electronics
Science 327 , 1601-1602 (2010) - Keimer, B.; Kivelson, S. A.; Norman, M. R.; Uchida, S.; Zaanen, J.
From quantum matter to high-temperature superconductivity in cooper oxides
Nature 518 , 179-186 (2015) - Kim, B. J.; Jin, H.; Moon, S. J.; Kim, J.-Y.; Park, B.-G.; Leem, C. S.; Yu, J.; Noh, T. W.; Kim, C.; Oh, S.-J.; Park, J.-H.; Durairaj, V.; Cao, G.; Rotenberg, E.
Novel Jeff = 1/2 Mott State Induced by Relativistic Spin-Orbit Coupling in Sr2IrO4
Physical Review Letters 101, 076402 (2008) - Kim, B. J.; Ohsumi, H.; Komesu, T.; Sakai, S.; Morita, T.; Takagi, H.; Arima, T.
Phase-Sensitive Observation of a Spin-Orbital Mott State in Sr2IrO4
Science 323, 1329-1332 (2009) - Matsuno, J.; Ihara, K.; Yamamura, S.; Wadati, H.; Iskii, K.; Shankar, V. V.; Kee, H.-Y-; Takagi, H.
Engineering a Spin-Orbital Magnetic Insulator by Tailoring Superlattices
Physical Review Letters 114, 247209 (2015) - Takayama, T.; Kato, A.; Dinnebier, R.; Nuss, J.; Kono, H.; Veiga, L. S. I.; Fabbris, G.; Haskel, D.; Takagi, H.
Hyperhoneycomb Iridate β-Li2IrO3 as a Platform for Kitaev Magnetism
Physical Review Letters 114 , 077202 (2015) - Jackeli, G.; Khaliullin, G.
Mott Insulators in the Strong Spin-Orbit Coupling Limit: From Heisenberg to a Quantum Compass and Kitaev Models
Physical Review Letters 102 , 017205 (2009) - Fujiyama, S; Ohsumi, H.; Komesu, T.; Matsuno, J.; Kim, B. J.; Takata, M.; Arima, T.; Takagi, H.
Two-Dimensional Heisenberg Behavior of Jeff = 1/2 Isospins in the Paramagnetic State of the Spin-Orbital Mott Insulator Sr2IrO4
Physical Review Letters 108 , 247212 (2012) - Chen, Y.; Lu, Y.-M.; Kee, H.-Y.
Topological crystalline metal in orthorhombic perovskite iridates
Nature Communications 6 , 6593 (2015) - Kitaev A.
Anyons in an exactly solved model and beyond
Annals of Physics 321 , 2-111 (2006)
Contact

Hidenori Takagi
Prof. Dr.Head of Institute