If several orbitals contribute to low-energy states of a transition metal oxide and if Coulomb repulsion is strong, charge fluctuations are suppressed and the Mott insulator resulting for one electron per site be described by a Kugel-Khomskii-type model [1], where spin spin and orbital degrees of freedom become formally almost equivalent. Excitations give information about the quantum dynamics, e.g., magnons in ferromagnetic manganites show that the main impact of alternating orbital order is a reduced magnon band width [2]. Apart from this reduced band width, the orbital background does not show up in the magnon dispersion, which implies that one can describe this situation by decoupling spins and orbitals in a mean-field approximation.
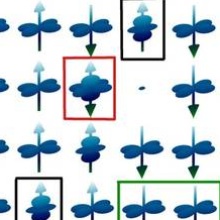
The analogous situation to a ferromagnet with alternating orbitals, but with reversed roles for spins and orbitals, is a ferro-orbitally ordered antiferromagnet, see the first row of the figure to the left. Here, the orbital degree of freedom is "polarized" like the spin the ferromagnet and the spins alternate. The analogon to a spin flip is then an orbital excitation. The excitation can move (third and fourth rows) via virtual excitations with doubly occupied sites (second row). In the fourth row, "magnetic" and "orbital" parts of the original excitations have moved apart [3], in a similar manner to spin-charge separation undergone by a hole in an antiferromagnetic (AF) chain.
Indeed, it turns out that the situation of the orbital excitation can be mapped onto the case of a hole moving in an AF background, at least for small Hund's rule coupling. As a consequence, this reversed situation leads to fundamentally different excitation spectra than the magnon case mentioned above, as can be seen in the figure to the right, where the spectrum obtained via the mapping is compared to the the line one would obtain in the mean-field decoupling. There are signature of spin-"charge" separation in one dimension, the periodicity of the dispersion clearly reflects the doubled unit cell of the AF background and additional incoherent features arise [3,4]. The decisive impact of the lowered symmetries in the orbital sector is thus revealed in the differences between magnons and orbital excitations. Recently, spin-orbit separation has been observed in resonant inelastic x-ray scattering (RIXS) for precisely this case, ferro-orbital and antiferromagnetic one-dimensional chains in Sr2CuO3 [5].
The same mapping and analysis have also been applied to an orbital excitation in the two-dimensional iridate Sr2IrO4. In this system, spin-orbit coupling is very strong, so that the half-filled orbital consists of eigenstates of the total angular momentum with j=1/2 rather than of spins in an orbital. Nevertheless, the orbital excitation into the higher levels with j=3/2 can again be mapped onto a hole moving in an AF background, here with an additional orbital flavor. The mapping and the evaluation of the spectral density using the self-consistent Born approximation give excellent agreement with RIXS data [6].
We also investigate the impact of core-hole properties on the spectra, using numerical techniques [7]. Open questions in this context are the impact of stronger Hund's rule which couples the spin of the excited electron to the background.
[1] K.I. Kugel and D.I. Khomskii, Sov. Phys. Usp. 25, 231 (1982).
[2] F. Moussa, M. Hennion, J. Rodriguez-Carvajal, H. Moudden, L. Pinsard, and A. Revcolevschi, Phys. Rev. B 54, 15149 (1996).
[3] K. Wohlfeld, M. Daghofer, G. Khaliullin, J. van den Brink, Phys. Rev. Lett. 107, 147201 (2011).
[4] K. Wohlfeld, M. Daghofer, G. Khaliullin, and Jeroen van den Brink,arXiv:1111.5522.
[5] J. Schlappa et al., Nature 485, 82 (2012).
[6] Jungho Kim, D. Casa, M. H. Upton, T. Gog, Young-June Kim, J. F. Mitchell, M. van Veenendaal, M. Daghofer, J. van den Brink, G. Khaliullin, B. J. Kim, Phys. Rev. Lett. 108, 177003 (2012).
[7] S. Kourtis, J. van den Brink, M. Daghofer, Phys. Rev. B 85, 064423 (2012).
Contact

Sebastian Loth
Prof. Dr.Head of Institute FMQ1 (managing director)