The oldest known "topologically nontrivial" phase are integer quantum Hall states, which are characterized by a quantized invariant and thus robust against distortions of the system. As a consequence, the quantization of the Hall conductance is extremely precise and the von-Klitzing constant is thus used as a standard for electrical resistance. Analogous states can also arise by breaking of time-reversal symmetry by other means that by a magnetic field [1], e.g. via spin-orbit coupling, as in topological insulators [2].
Recently, it was proposed that nearly flat and topologically nontrivial bands in lattice models might allow an analogous generalization of fractional quantum-Hall (FQH) states [3]. If the Coulomb repulsion is both large compared to the band width and small compared to the gap separating the band from its neighbors, it can stabilize FQH-like states.
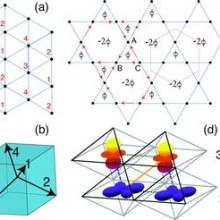
We were able to show that an orbital degree of freedom can substantially flatten bands, which have a topological character due to an "effective magnetic flux" induced by non-coplanar "chiral" magnetic order [4]. In the figure to the right, the spin pattern of the chiral phase on the triangular lattice is schematically shown: The four spin of the unit cell, in (a), point to the corners of a tetrahedron, see (b); the chirality Si(SjxSk) enclosed by three spins around a triangular plaquette is non-zero.
We showed this effect for a chiral state on both the triangular and the kagome lattices, and find that is work for either eg or t2g orbitals. The eg orbitals are also shown in panel (d), where we illustrate how octahedra in perovskites build a triangular lattice.
In our first study, we had built on the fact that frustrated lattices are known to be able to support chiral magnetic phases. We were then able to show that a chiral phase with topologically nontrivial and very flat bands arises self-consistently in a strongly correlated three-orbital model for t2g orbitals on a triangular lattice [5]. The figure to the right shows an example for the one-particle bands obtained in mean field. Here, periodic boundary conditions were used along one directions, and open along the other, i.e., we use a tube. Momentum is thus only conserved along the first direction and gives the x-axis of the plot. For each kx, one finds several bands, their width is determined by the dispersion along the y-direction. One clearly sees some very flat bands of mostly a1g character, especially the one directly above the chemical potential. The red and blue dashes and dots decorate edge states living on the top and bottom edges of the tube, which are absent for fully periodic boundary conditions. They connect the bands above and below the chemical potential and are an indication of the topologically nontrivial character of the bands.
The band-flattening effect is very robust in this model, both the chiral phase and the nearly flat bands arise for large parameter regions. As the flat band is well separated from other bands, one can map it onto an effective one-band model with a two-site unit cell. The two-site unit cell is given by the chiral magnetic order and allows the nontrivial topological character. The flatness of the band is caused by effective longer-range hopping due to virtual excitations.
The much simpler one-band model can be treated on finite clusters with exact diagonalization and we were indeed able to establish signatures of FQH-like states for a large number of filling fractions [5,6]. These Fractional Chern insulators reveal themselves through a variety of signatures, both in the energy levels and in a fractional value of the Hall conductance. Of course, FCI states compete with other phases; as they rely on long-range Coulomb repulsion, charge-density waves are obvious competitors. We study the stability of both phases and find that the charge-density wave wins if it is favored by Fermi-surface nesting. If the Fermi surface is not well nested, even quite dispersive bands can host a fractional Chern insulator [6].
[1] F. D. M. Haldane, Phys. Rev. Lett. 61, 2015 (1988).
[2] For review articles, see M. Hasan and C. Kane, Rev. Mod. Phys. 82, 3045 (2010); X.-L. Qi and S.-C. Zhang, Rev. Mod. Phys. 83, 1057 (2011).
[3] E. Tang, J.-W. Mei, and X.-G. Wen, Phys. Rev. Lett. 106, 236802 (2011); K. Sun, Z. Gu, H. Katsura, and S. D. Sarma, Phys. Rev. Lett. 106, 236803 (2011); T. Neupert, L. Santos, C. Chamon, and C. Mudry, Phys. Rev. Lett. 106, 236804 (2011).
[4] J. W.F. Venderbos, M. Daghofer, J. van den Brink, Phys. Rev. Lett. 107, 116401 (2011).
[5] J. W.F. Venderbos, S. Kourtis, J. van den Brink, M. Daghofer, Phys. Rev. Lett. 108, 126405 (2012).
[6] S. Kourtis, J. W.F. Venderbos, M. Daghofer, Phys. Rev. B 86, 235118 (2012).
Contact

Sebastian Loth
Prof. Dr.Head of Institute FMQ1 (managing director)